
Saturs
- Zipf likums paskaidroja
- Pamata eksperiments
- Zipf likums Steam tirgos
- Ko mēs varam uzzināt par Steam?
- Secinājumi
Pirms neilga laika mans draugs ieteica skatīties Vsauces video par Zipf likumu, Pareto principu un to noslēpumaino izskatu apkārt mums. Lūk, mazliet pievilcīgāks, lai iegūtu savu uzmanību - 80% no visiem cilvēkiem dzīvo 20% no populārākajām pilsētām; 80% no visas zemes pieder 20% bagātāko saimnieku; 80% no visiem atkritumiem atrodas visaugstākajā 20% trashiest ielās - kā to paredz Zipf likums un Paretos princips.
Nepietiekami? Nu, kā es atklāju vakar, trušu caurums neapstājas tur ... Pilns skepticisms, es nolēmu apskatīt, cik daudz laika cilvēki pavada, spēlējot Steam spēles ... Nu. 80% cilvēku laika tiek pavadīti spēlējot 20% no populārākajām spēlēm ... Interesanti? Nu, lasiet tālāk, ir vairāk par šo stāstu.
Pulkstenis vairāk nekā 20 min., Vsauces centieni ir satriecoši, un izskaidro daudz lielo attēlu par Zipf, tomēr viņš ir ļoti kautrīgs, parādot mums galveno mehānismu, kas tiek plaši uzskatīts par ieguldījumu, kāpēc Zipf darbojas kā tā darbojas. Tāpēc, pirms mēs turpinām, es to gribētu īsi izskaidrot.
Zipf likums paskaidroja
Ir vairāki konceptuāli veidi, kā izskaidrot 20/80 principa intuīciju. Manuprāt, labākais piemērs ir viens par Mēness krāteriem.
Pamata eksperiments
Tātad, iedomājieties, ja jūs gribēsiet, ka ir neskarts Mēness - pilnīgi gluda virsma. Tagad, teiksim, ka ir daži nejauši izmērīti asteroīdi, kas skāra Mēnesi nilly. Kad pirmie asteroīdi nolaida, tas atstāj krāteri. Tagad vēl viens hit, atstājot krāteri citur. Katrs krāteris ir daļa no kopējās virsmas platības, tāpēc pastāv iespēja, ka nākamais nejaušais asteroīds nonāks tuvu esošajam krāterim un pievienosies tai, veidojot grupu. Jauna asteroīda iespēja nokļūt kādā krāterī ir proporcionāla krāteriem un asteroīdiem. Tas nozīmē, ka nākamais nejaušais asteroīds, visticamāk, pievienosies lielākajai esošajai grupai, padarot to vēl lielāku. Kumulatīvs process, kas pēc tam izveido bagātīgu, bagātāku nabadzīgu un vienaldzīgu mehānismu.
Paturiet to prātā, jo domājams, ka tas ir vispārējs skaidrojums tam, kāpēc Zipfs likums darbojas ar šādu noslēpumainu universālumu. Asteroīdu piemērs ir diezgan vienkāršs, tomēr jautājums ir par to, kas notiks daudzu atkārtojumu laikā
Mazliet apjukums?
Nu, es gif, lai vadītu šo sākotnējo punktu mājās. NB! grafiks tiks apspriests vēlāk, vienkārši mēģiniet attēlot eksperimentu.

Ja mēs novērojam faktisko Mēness, izrādās, ka, palielinoties asteroīdu daudzumam, novērotie krāteru diametri palielinās tā, ka 20% lielāko krāteru top 80% no visas virsmas platības.
Tā kā mēs dodamies uz vairāk asteroīdiem, vispopulārāko grupu izplatīšana vismazāk populārām grupām tuvojas kādam "ideālam sadalījumam" ar šo 20/80 īpašumu - Pareto izplatīšanu. Ja jūs veicat matemātiku, izrādās, ka (visumā), ja lielākajai grupai ir N izmērs, otra lielākā grupa ir ap N / 2 lielumu, trešo N / 3 un tā tālāk. To sauc par Zipf likumu. Dīvainā lieta ir Zipf likums un Pareto izplatīšanas darbi, kas rada nežēlīgu daudzumu elementu (asteroīdu) un grupu (krāteru kopas). Protams, ir izkropļojumi un nejauši traucējumi, bet vispārējā tendence ir nenoliedzama.
Es ceru, ka jūs redzēsiet, kā asteroīdi, kas biežāk skar lielos krāterus uz Mēness, savienojas ar pilsētām, kas ir pievilcīgākas, ja tajos jau dzīvo vairāk cilvēku. Tomēr ir jāsaprot, ka pilsētas ir tālu no vienīgajām "grupām", kas darbojas saskaņā ar Zipf.
Lūk, daži piemēri no Markas Newmansa pētījumiem par Pareto sadalījumiem. NB! Grafiki ir log-log skalā, kas izlīdzina līkņu hiperbolisko formu, parādot gandrīz lineāru sakarību.
Sākotnējā y = aX ^ (- b)
Abu pušu žurnāli => log y = log a - b log X
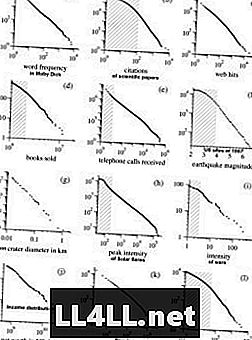
Interesanti, ka to pašu tendenci parāda arī reliģiskās kultas ... Lielākā daļa no šīm parādībām ir tikai šī "lielo grupu-iegūt-lielāka" tendence. Līdz ar to Zipf likums ir noturīgs mehānismos, kur elementu preferences ir pozitīvi saistītas ar grupu lielumu (tas nozīmē, jo lielāka grupa, jo lielāka iespēja, ka tā pieaugs). Tāpēc es gribētu domāt par grupām kā kopām un elementiem kā kopu veidotājiem.
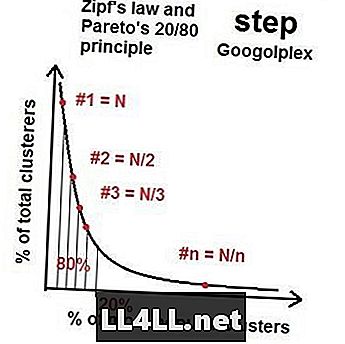
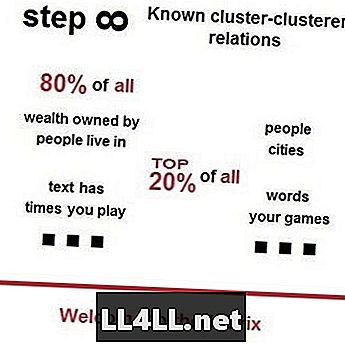
Zipf likums Steam tirgos
Aizdomīgs par pēdējo? Šeit ir laiks, ko cilvēki tērē populārākajām spēlēm uz Steam. Dati no SteamSpy.
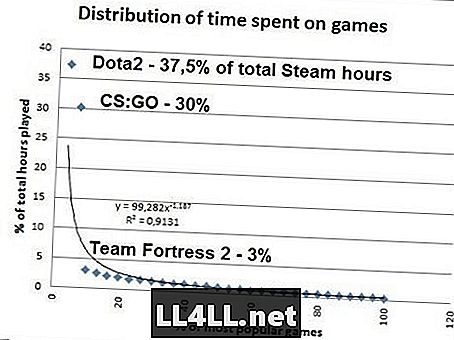
Ja jūs veicat matemātiku, izrādās, ka 20% no populārākajām Steam spēlēm veido 80% no kopējā spēles apjoma, tāpēc Pareto 20/80 noslēpums šeit darbojas kā šarms. Zipf ir taisnība, CS: GO 37,5% / 2 = 18,8% no kopējā laika, nevis 30%. Bet malā no šī iznākuma (STOP PLAYING) CS: GO), Zipf līdzīgā izplatība ir skaidri redzama.
Šeit ir pārdoto kopiju skaits populārākajām spēlēm.
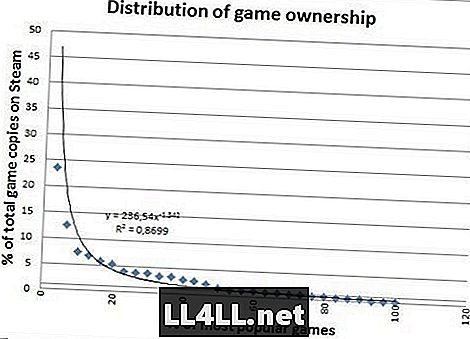
Izskatās daudz nicer eh? Pārdotajām kopijām nav lielas izejas, tāpēc tas ir ļoti labi piemērots, kas ir ievērojama atšķirība. Tomēr no pēdējo divu grafiku atšķirībām ir kaut kas interesantāks.
Vai jūs pamanāt, kā "astes", kas iet pa labi, otrajā grafikā ir tauki? Vienkārši sakot, tas nozīmē, ka "salīdzinoši nepopulārās" spēles patiesībā ir daudz populārākas nekā iepriekšējā parauglaukumā.
Faktiski izrādās, ka 20% no populārākajām spēlēm veido tikai 60% no pārdošanas apjoma, salīdzinot ar 80% no spēles. Interesanti? Jūs bet savu ass to.
Ko mēs varam uzzināt par Steam?
Nu, tas, ka spēles popularitāte izriet no Pareto izplatīšanas, mums saka, ka patiešām ir kāda pozitīva tīkla ietekme, kas ļauj spēlētājiem izvēlēties spēles, kuras jau spēlē vairāk cilvēku. Kāda atšķirība starp astes taukiem liecina, ka tvaika lietotāji ir daudz "neredzīgāki", pērkot spēles, nekā tie, kad tie spēlē.
Padomājiet par to - jo vairāk cilvēku pērk spēles, neskatoties uz "pašreizējo populāro viedokli", jo vairāk izlīdzinās Pareto izplatīšana, jo mazāka iespēja, ka lielās spēles turpinās pieaugt. Ja neviens neradīja žurku mucu par to, cik daudz cilvēku jau spēlē spēli, un visu spēļu pieejamība bija vienāda, tad mēs sagaidām, ka 20% no populārākajām spēlēm veidos aptuveni 50% no pārdošanas un spēles laika (piemēram, pieņemot, ka individuālās preferences ir parasti izplatās).
Secinājumi
Līdz ar to ir divi faktori, kas veicina Pareto izplatīšanu Steam tirgos - cik inovatīvi ir attīstītāji (cik jauni Mēness krāteri tiek veidoti) un cik daudz spēlētāju (asteroīdu) vērtē pašreizējo grupas lielumu, izvēloties grupu, kurai pievienoties . Kā izrādās, spēlētāji, iegādājoties spēles, ir ļoti lielas, neredzīgas, bet tieši pretēji, kad tās spēlē. Atdzesē?
Ja vēlaties uzzināt vairāk par Zipf likumu un varas likumu sadalījumu, šeit ir jauka lekcija. Turklāt, pārliecinieties, ka apskatīsiet Newman papīru!
Ja vēlaties uzzināt vairāk par šāda veida precēm, drīz vien mēģināšu pievienoties šim novērojumam uz modeli, kas parāda, ka vairāk populārām spēlēm ir augstākas cenas (kas piesaista spēlētāju izvēli pievienoties lielākām grupām). Skatīt rakstu šeit. Raksts „Piece De Resistance” mēģinās apvienot šīs teorijas kopā, izskaidrojot, kā multiplayer spēles, sociālie tīkli un pilsētas faktiski ir visas pret konkurenci vērstas preces ar tīkla ietekmi (jo vairāk cilvēku patērē labu, jo vairāk katra individuālā patēriņa priekšrocība) viņiem ir tiesības ar šo Zipfian noslēpumaino miglu ...
Līdz tam - baudiet sevi!
P.S. Pop komentārā ar jautru ideju par 20/80 attiecībām, kuras, jūsuprāt, varētu būt patiesas.
Raktuves ir:
80% cilvēku nostalģijas izraisa 20% viņu vislaimīgāko atmiņu (faktiski pierādīts, ka likme cilvēkiem aizmirst informāciju)
80% masas koncentrējas 20% no lielākajiem kosmosa objektiem (kas faktiski pierādīti gravitācijas spēka izplatīšanai)
Un protams
80% no jūsu tualetes netīrumiem nāk no 20% no tā, ko ēdat (bez akadēmiskiem pētījumiem)